Why the fundamental theorem of calculus is gorgeous? In the ancient history, it’s easy to calculate the areas like triangles, circles, rectangles or shapes which are consist of the previous ones, even some genius can calculate the area which is under a closed region of a parabola boundary by indefinitely exhaustive method. Actually it’s the calculation of integrals with the help of the definition of definite calculus. Such as we caculate the area bounded by the \(f(x)=x^2\), axis \(x\) and axis \(y\), which is OAB.

Definition of definite calculus, we use this to stand for the area by the standard Leibniz notation. \[ \int_a^b f(x)dx = \lim_{\max\Delta x_k\to0}\sum_{k=1}^nf(x^*_k) \Delta x_k \] Assume the point B is \((b, 0)\), cut the \(OAB\) into n rectangles. The area of the first one is \((\frac{b}{n})(\frac{b}{n})^2\), the second is \((\frac{b}{n})(\frac{2b}{n})^2\) , and the nth is \((\frac{b}{n})(\frac{nb}{n})^2\) , so we have the S, apparently, \(\Delta x_k = \frac{b}{n}\)
\[ S = (\frac{b}{n})(\frac{2b}{n})^2 + (\frac{b}{n})(\frac{nb}{n})^2 + ... + (\frac{b}{n})(\frac{nb}{n})^2 \]
\[ S=(\frac{b^3}{n^3})(1^2+2^2+...+(n-1)^2+n^2) \]
\[ S=(\frac{b^3}{n^3})(\frac{n(n+1)(2n+1)}{6})=b^3(\frac{1}{6}+\frac{1}{6n})(2+\frac{1}{n}) \]
When \(\Delta x_k\to0, n\to\infty, S=\frac{b^3}{3}\).
But what about the calculation of \(f(x)=x^5\), \(f(x)=cosx\), \(f(x)=(1+\frac{1}{x^5})\) , it’s not so easy with previous primary method to get the result. We have to use the fundamental theorem of calculation which is described as If \(f(x)\) is a continuous function on a closed interval \([a,b]\), \(F(x)\) is any antiderivative of \(f(x)\), in another word \(\int f(x)dx=F(x)+c\), then \(\int_a^b f(x)dx = F(b)-F(a)\).
Now we have a weapon to solve the previous problem in a flash moment. \(\int_0^b x^2dx = F(b) = \frac{b^3}{3}\)
How did the mathematicians get the FTC? (Fundamental theorem of calculus).
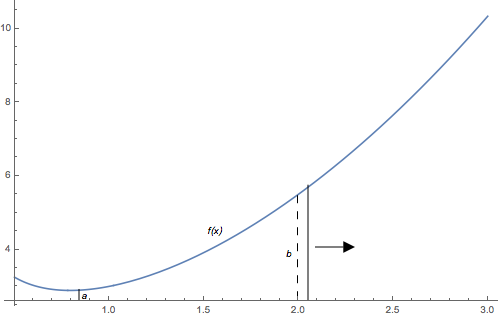
Now we need to calculate the area between edge a and b, b is moving to the right, so the area A is a function of x, so we note the area \(A(x)\), so \(\Delta A(x)=A(x+\Delta x)-A(x)=f(\bar x)\Delta x\), so \(A'(x)=f(x)\), which means \(A(x)=F(x)+c\), \(F(x)\) is a antidirevative of \(f(x)\). When edge a, b coincide, the area is 0, \(A(a)=0\), so we have \(A(a)=F(a)+c\) and \(c=-F(a)\), we get \(A(b) = \int_a^b f(x)dx = F(b) - F(a)\).
When we need to calculate the area, we just need to find the indefinite integral first, then do some basic calculation. The FTC is a milestone in the development of mathematic.