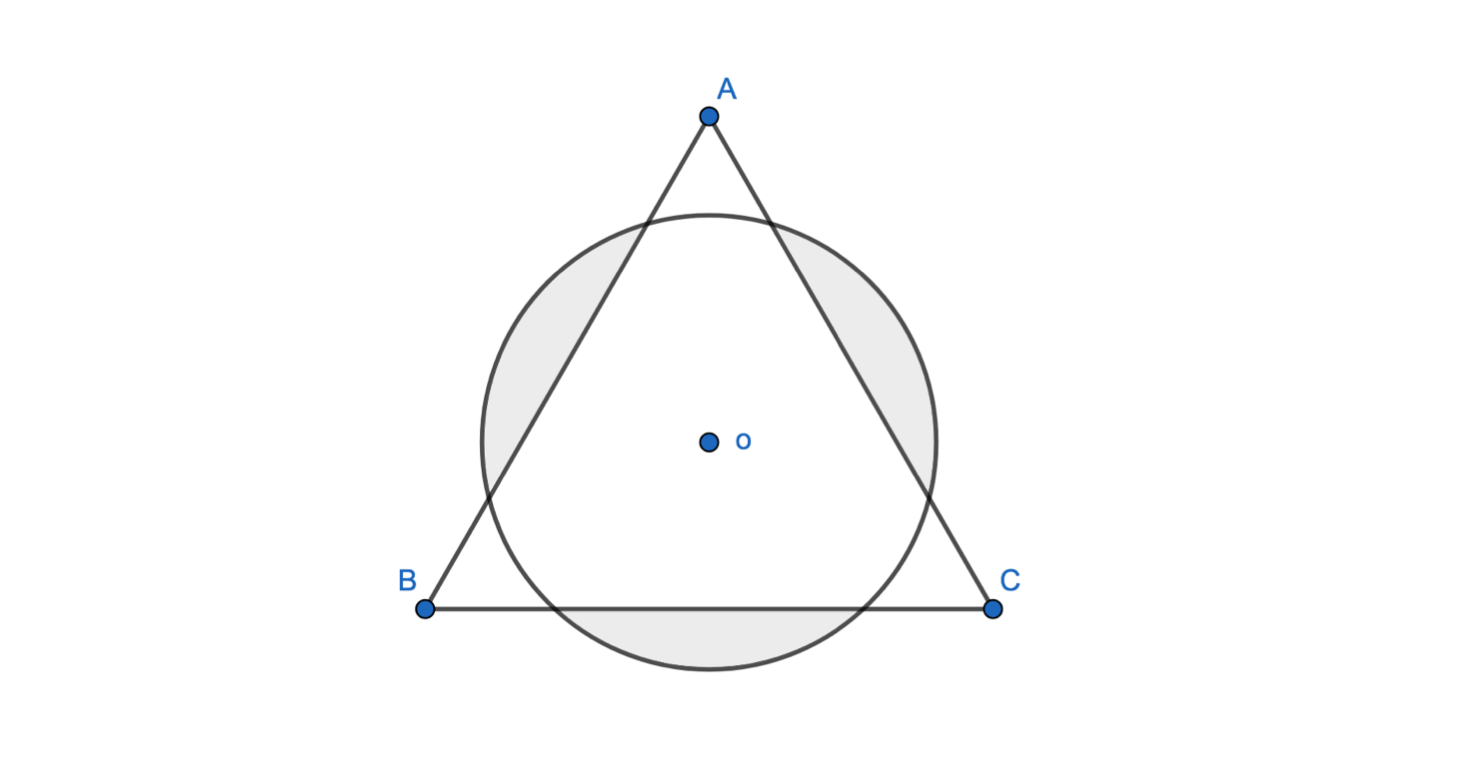
已知圆的半径为4，等边三角形的边长为10，且图中三部分阴影部分面积相等，求阴影部分的面积。（6年级），这道六年级的数学题，小学六年级的知识肯定是不会做的，除非使用量角器，并且同时量出来的角度是90度，解这个题并不需要多深的数学知识，之所以记录下来是因为我自己解这道题时思考的顺序很有意思。

解法1: 初等三角

题中说明三个阴影部分面积相等，显然得出结论圆心与等边三角形中心重合（证明略），所以已知条件为，\(假设∠DoF=α，∠EoF=\frac{2π}{3}，∠DoE=\frac{2π}{3}-α，AD=x，DF=y，AB=10，r=4\)

\(Sin(\frac{\frac{2}{3}π-α}{2})=\frac{\frac{x}{2}}{r}=\frac{x}{8}\)	方程1
\(Sin(\frac{α}{2})=\frac{\frac{y}{2}}{r}=\frac{y}{8}\)	方程2
\(2x+y=10\)	方程3

之后就是解这个方程组了，之前我错误的估计了方程组是比较难解的未知数耦合的非线性方程，其实最简单的三角函数展开就行了。令\(β = \frac{α}{2}\)，方程组变为， \[sin(\frac{ π }{3}-β)=\frac{x}{8}，sinβ=\frac{y}{8}，2x+y=10\] 合并成一个方程 \[16sin(\frac{ π }{3}-β)+8sinβ=10\] 展开得到 \[8\sqrt{3}cosβ=10，α=2β=2arccos(\frac{5}{4\sqrt{3}})≈1.528（角度制87.59°），β=0.764，x≈2.231，y≈5.535\] 最终面积为 \[SB=3*(S_{扇形DoF}-S_{ΔDoF})=3*(πr^{2}*\frac{α}{2π}-\frac{1}{2}*r^{2}sinα)≈12.66\]

解法2: 定积分

简单粗暴，求面积\(3*(S_{EHMGI}-S_{EHGI})\)，此处坐标原点的选取对求解非常重要。选取不好积分非常难积。

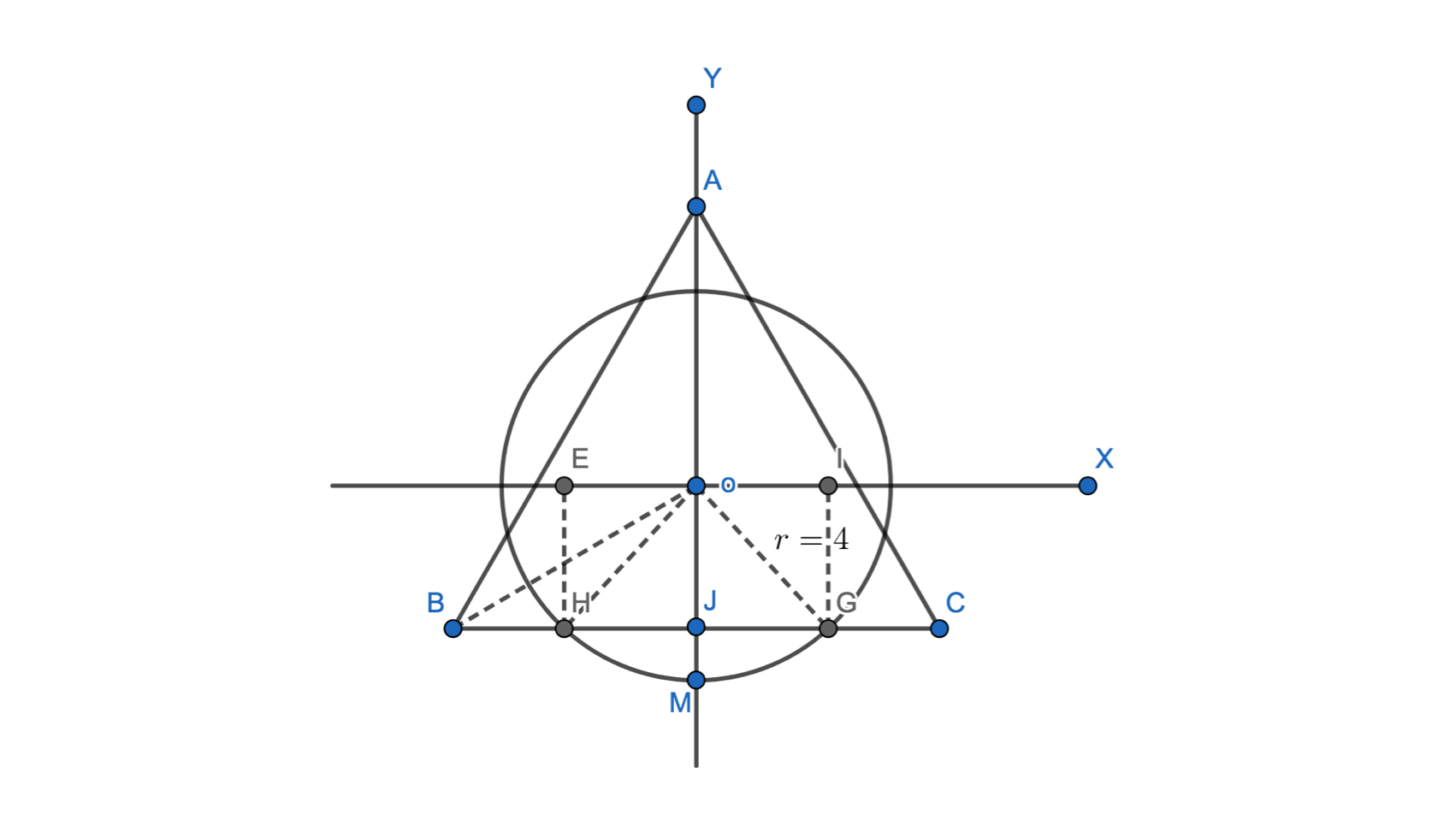
\(S_{EHMGI}=\int_a^b f(x)dx=\int_a^b (-\sqrt{16-x^{2}})dx\)

其中a对应H的横坐标， b对应G的横坐标

设\[OJ=m，∠OBJ=\frac{π}{6}，OB=2m，BJ=5，计算得到，a=-\sqrt{\frac{23}{3}}，b=\sqrt{\frac{23}{3}}\] 以下就集中搞这个积分。 \[令x=4sin(u)，dx=4cos(u)du，u=arcsin(\frac{x}{4})\] \[-\int (\sqrt{16-x^{2}})dx=-\int{ }\sqrt{16-16sin^2u}·4cosudu=-16\int{ } cos^2udu\] 三角变换得 \[-16\int{ } cos^2udu=-8\int{ }(cos2u+1)du=-4sin(2u)-8u+c=-8sinu·cosu-8u+c\] 把\(u=arcsin(\frac{x}{4})\)带入得 \[-8sinu·cosu-8u+c=-2x\sqrt{1-\frac{x^{2}}{16}}-8arcsin\frac{x}{4}+c\] 最终求定积分为-20.22，则面积为\(S_{EHMGI}≈20.22\)，\(S_{EHGI}=OJ*2HJ=2\sqrt{\frac{25}{3}}\sqrt{\frac{23}{3}}≈15.99\)，最终面积约为12.69

解法3: 初中阶段三角函数定义

在求定积分的上下限时，其实已经直接可以算面积了。求得结果与第一种解法完全一样。10000点暴击。 \[OJ=\sqrt{\frac{25}{3}}，cos∠JoH=\frac{OJ}{OH}=\frac{5}{4\sqrt{3}}，∠JoH=arccos\frac{5}{4\sqrt{3}}≈0.764\]