Consider the equation \(x^3-3x-5=0\), we can get the exact solution just as the quadratic equations. But it’s not easy to remember the formula. And for some equations like, \(x-cosx=0\), there’s even no way to get the analytic solutions. As an engineer, sometimes, we just require a acceptable numerical solution that is accurate to a reasonable number of decimal places.
Plot the function
Sketch the function \(f(x)=x^3-3x-5\) , the derivative of function \(f(x)\) is \(f'(x)=3x^2-3\),
| x | f(x) or f’(x) |
|---|---|
| \(x=1 , x=-1\) | \(f'(x)=0\) |
| \(x<-1, x>1\) | \(f'(x)>0\) |
| \(-1<\)x\(<1\) | \(f'(x)<0\) |
| \(x=-1\) | \(f(x)=-3\) |
| \(x=1\) | \(f(1)=-7\) |
| \(x=2\) | \(f(2)=-3\) |
| \(x=3\) | \(f(3)=13\) |
The second derivative is \(f''(x)=6x\), so the point \((0, -5)\) is the point of inflection, when x < 0, the chart concave down, x > 0, the chart concave up.
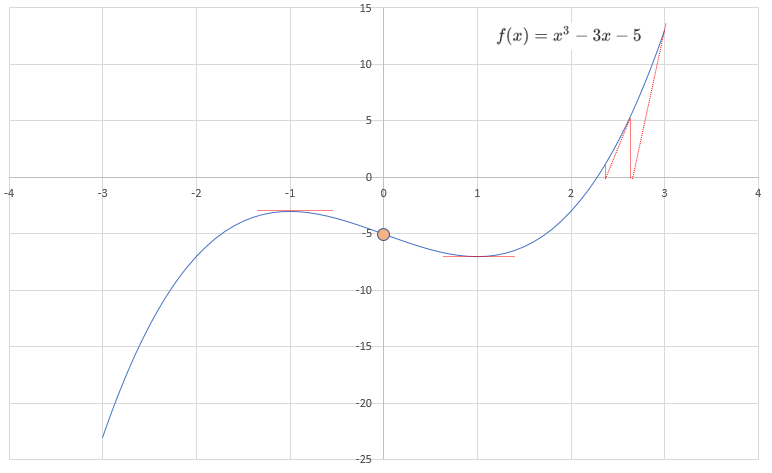
\(f(2)=-3, f(3)=13 \Rightarrow x_{0} \in (2, 3)\), we start from the point \(x_{1}=3\),
\[ f'(x_{1})=\frac{f(x_{1})-0}{x_{1}-x_{2}} \Rightarrow x_{2}=x1-\frac{f(x_{1})}{f'(x_{1})} \]
\[ f'(x_{2})=\frac{f(x_{2})-0}{x_{2}-x_{3}} \Rightarrow x_{3}=x2-\frac{f(x_{2})}{f'(x_{2})} \]
\(...\)
we get the x by multiple calculation of \(x_{n}\), \(x_{2}=2.458333\), \(x_{3}=2.294310\), \(x_{4}=2.279144\), \(x_{5}=2.279018\)
and \(f(x_{5})=-0.000009\), and \(x_{5}\) is acceptable as the root of the equation.